在《復仇者三》中,反派 Thanos 的目標是把全宇宙的人口砍半,他認為這可以解決人口過剩造成的各種社會問題。但是如果學過基本的生態學或人口學,就會發現他的想法完全錯誤。我們來看看他的手段會造成什麼問題。
首先,我們來看看基本的指數成長:
這是最基本的人口模型,這條公式說:在任一時間(t),人口變化率( )取決於當時的人口(N)以及單位人口成長率(r)。
)取決於當時的人口(N)以及單位人口成長率(r)。
例如這裡有 4 個人(N = 4),每個人生 2 個小孩(r = 2),那就會增加 8 個人。如果不是生兩個小孩,而是死一半的人(r = - 1/2),那就會減少2個人。只要 r > 0 人口就會持續成長。
這是最基本的人口模型,這條公式說:在任一時間(t),人口變化率(
 )取決於當時的人口(N)以及單位人口成長率(r)。
)取決於當時的人口(N)以及單位人口成長率(r)。 例如這裡有 4 個人(N = 4),每個人生 2 個小孩(r = 2),那就會增加 8 個人。如果不是生兩個小孩,而是死一半的人(r = - 1/2),那就會減少2個人。只要 r > 0 人口就會持續成長。
這公式只告訴我們人口變化率,如果要知道總人口是多少的話,我們要解微分方程。(對數學沒興趣的人可以跳過灰色的部份)
先把 N 移到左邊、dt 移到右邊:

然後兩邊取積分:

積出來是:

兩邊取指數後得到:

如果代入 t = 0,我們可以看出來 ec 其實就是人口的起始大小,可以改用 N0 來表示。因此我們可以解出:
Thanos 想要把人口減半,但是 r 沒有變,所以人口還是會持續無限成長到爆炸。人口減半後要多久才會回到原本的大小呢?如果拿被砍半的人口當作起始點,想知道要多久人口才會變成起始值的兩倍,那就是 N = 2 N0 ,求解 t 是多少。先把左邊的 N 代換成前面解出來的人口大小公式:

先把 N 移到左邊、dt 移到右邊:

然後兩邊取積分:

積出來是:

兩邊取指數後得到:

如果代入 t = 0,我們可以看出來 ec 其實就是人口的起始大小,可以改用 N0 來表示。因此我們可以解出:
Thanos 想要把人口減半,但是 r 沒有變,所以人口還是會持續無限成長到爆炸。人口減半後要多久才會回到原本的大小呢?如果拿被砍半的人口當作起始點,想知道要多久人口才會變成起始值的兩倍,那就是 N = 2 N0 ,求解 t 是多少。先把左邊的 N 代換成前面解出來的人口大小公式:

把兩邊的 N0 消掉(人口不是 0),然後取對數後變成:
把 r 移到右邊,解出:
2017年,地球的人口成長率是每年增加 0.011,再代入ln 2 = 0.69315,算出來大約是 63 年。計算過程中 N0 被消掉了,這表示不管地球上有多少人,若 Thanos 把人口減半,只要 63 年過後人口就會回復。這是假設 r 值不變,人們沒有因為人口減半資源很多所以決定多生一些小孩、或是因為擔心環境危險所以不生小孩。
有的人可能會說:不對啊!人類的人口成長率在降低,在工業化之後的先進國家,生小孩不再是幫忙打獵或下田,反倒要花費許多時間金錢,所以生率都會下降。換句話說,我們應該接近人口承載上限(K)了。好,我們來看看如果有人口承載上限的情況下,Thanos 會造成什麼影響。這是 Logistic Growth 模型,中文有時翻作邏輯型成長、S 型成長、邏輯斯蒂模型等等:
比起前一個模型,主要的差別就只是在算人口變化率時,人口成長率 r 會先乘以 ,然後再乘以現在的人口大小 N。這意思就是說當人口大小 N 上升到承載上限 K 時,實際的人口成長率
,然後再乘以現在的人口大小 N。這意思就是說當人口大小 N 上升到承載上限 K 時,實際的人口成長率 就會下降到 0;如果人口超過 K 時,
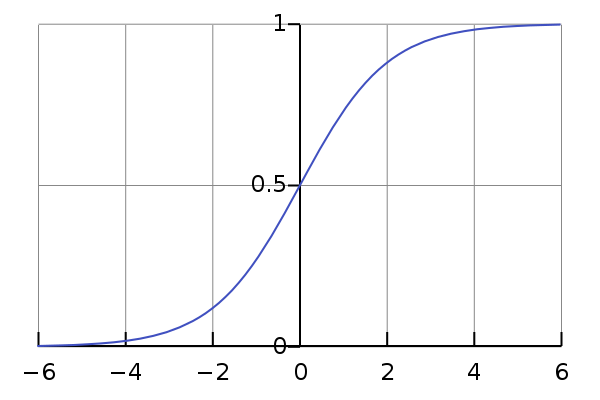
就會下降到 0;如果人口超過 K 時,  就會變成負的,於是人口會下降到 N = K。如果把圖畫出來,橫軸放時間,縱軸放人口,會得到這種形狀的曲線:
就會變成負的,於是人口會下降到 N = K。如果把圖畫出來,橫軸放時間,縱軸放人口,會得到這種形狀的曲線:
(不要管座標軸的數字)
把 r 移到右邊,解出:
2017年,地球的人口成長率是每年增加 0.011,再代入ln 2 = 0.69315,算出來大約是 63 年。計算過程中 N0 被消掉了,這表示不管地球上有多少人,若 Thanos 把人口減半,只要 63 年過後人口就會回復。這是假設 r 值不變,人們沒有因為人口減半資源很多所以決定多生一些小孩、或是因為擔心環境危險所以不生小孩。
有的人可能會說:不對啊!人類的人口成長率在降低,在工業化之後的先進國家,生小孩不再是幫忙打獵或下田,反倒要花費許多時間金錢,所以生率都會下降。換句話說,我們應該接近人口承載上限(K)了。好,我們來看看如果有人口承載上限的情況下,Thanos 會造成什麼影響。這是 Logistic Growth 模型,中文有時翻作邏輯型成長、S 型成長、邏輯斯蒂模型等等:
比起前一個模型,主要的差別就只是在算人口變化率時,人口成長率 r 會先乘以
 ,然後再乘以現在的人口大小 N。這意思就是說當人口大小 N 上升到承載上限 K 時,實際的人口成長率
,然後再乘以現在的人口大小 N。這意思就是說當人口大小 N 上升到承載上限 K 時,實際的人口成長率 就會下降到 0;如果人口超過 K 時,
就會下降到 0;如果人口超過 K 時,  就會變成負的,於是人口會下降到 N = K。如果把圖畫出來,橫軸放時間,縱軸放人口,會得到這種形狀的曲線:
就會變成負的,於是人口會下降到 N = K。如果把圖畫出來,橫軸放時間,縱軸放人口,會得到這種形狀的曲線:(不要管座標軸的數字)
我們先看人口變化率就好。人口為上限的一半的時候,人口上升最快。這可以很容易用微分等於零找極值來證明。先把右邊乘開:
然後解微分等於零:
解出:
三次微分是負的,所以我們知道這是最大值,不是最小值。或者也可以用配方法來找極值:
總之,在人口是承載上限的一半時,人口成長率來到最大值。對所有已經生活在承載上限的星球來說,Thanos 如果把人口砍半,正好讓人口爆發變成最快。
往好的方面想,人口成長最快表示這裡離人口上限還很遠,平均生活品質不錯,同時又有夠多人,找伴侶不會太辛苦,或許 Thanos 的想法沒錯。
但是前面提到的問題還在:隨時間過去,人口會慢慢回復到原本的大小。接下來我們來解方程式,算人口要多久才會回到被砍半之前的大小。回到一開始的模型,把 移到左邊,dt 移到右邊:
移到左邊,dt 移到右邊:
 移到左邊,dt 移到右邊:
移到左邊,dt 移到右邊:
左邊的分數相乘可以拆成兩個分數相加:
兩邊取積分:
得到:
把左邊兩個對數合併,然後取指數:
在這邊可以順便代入 t = 0 先解 ec:
回到上一步剛取完指數的部份,把左邊的分母移到右邊乘開:
有 N 的部份移到左邊,並把 N 提出來:
沒有 N 的部份移回右邊:
然後套入剛才先解好的 ec:
右邊分子分母同乘 ,稍加整理後可以得到:
,稍加整理後可以得到:
 ,稍加整理後可以得到:
,稍加整理後可以得到:
跟前面一樣,我們要算的是 N = 2 N0 時 t 是多少:
消掉 N0 ,把右邊的分母移到左邊:
把 ert 移到右邊:
右邊的 ert 提出來,其餘移到左邊:
取對數後解出:
我們不能假設 Thanos 在人口已經在承載上限時將人口減半,因為N0 = K/2,對數部份的分母變成零,算出來要無限久的時間,這是因為人口越靠近承載上限,成長率就越慢,所以永遠到不了上限。我們假設地球的人口是在 90% 上限好了,減半後 N0 = 0.45 K。
注意前一個模型用的 r = 0.011 不能直接套用,而是
 。這裡的 N 是還沒被砍半以前,用0.9 K 算:
。這裡的 N 是還沒被砍半以前,用0.9 K 算: 算出來是 r = 0.11,套進 t = 2.4 / r 後我們得到 21.8 年。沒錯!Thanos 大費週張要收集一堆石頭,包括時間之石,來讓人口減半,但是地球的人口可以輕易在 21.8 年的時間後回復原狀。這個時間之石好像沒辦法超脫時間的魔咒。



























沒有留言:
張貼留言